第二次学习AC自动机与第三次学习KMP (●’◡’●)

字符串不可战胜

以后我将只使用 AC自动机，比 KMP 简单好多啊。

AC自动机

利用 Trie 的结构 和 KMP 的思想构建 AC自动机。
注意：KMP的思想而不是思路或者代码

KMP的思想是失配后快速挪到下一个匹配位置。
所以我们在 AC自动机 上构建 fail 指针，也是这个作用，但是定义不一样。
KMP中 nxt 指的是最长的相同前后缀。
AC自动机中 fail 是所有模式串的前缀中匹配当前状态的最长后缀。
所以我们不能拿构建 nxt 的思路方法构建 fail。

怎么匹配？

通过走 Trie 树，如果失配了就跳 fail 指针来快速的匹配。

怎么构建 fail 指针？

广搜，所以我们处理到当前节点时，深度小于当前节点的已被处理完。
然后先跳父亲的 fail ，然后跳 fail 的fail 。
直到跳到的某个点有当前状态的出边，然后就指向出边的节点。
偷一张 OI-Wiki 的图：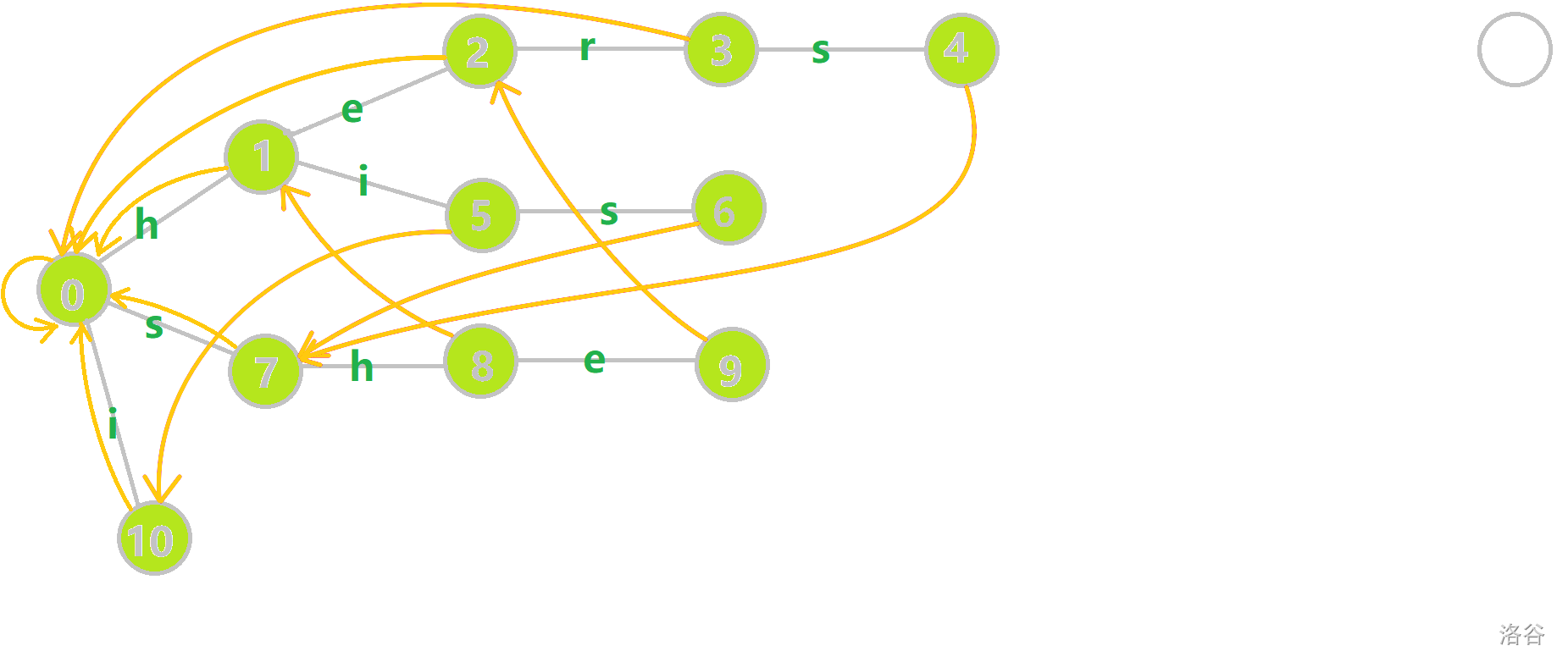

去看 6 节点的 fail 构建：
先跳到父亲节点 5 ，然后跳父亲的 fail 到 10 ，然后 10 没有 ‘s’ 这条出边，跳 10 的 fail 到 0，发现 0 有 ‘s’ 的出边，所以 6 的 fail 指向 7。
再偷一下 OI-Wiki 的代码：

void build() {
  queue<int> q;
  for (int i = 0; i < 26; i++)
    if (tr[0].son[i]) q.push(tr[0].son[i]);
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u].son[i]) {
        tr[tr[u].son[i]].fail = tr[tr[u].fail].son[i];
        q.push(tr[u].son[i]);
      } else
        tr[u].son[i] = tr[tr[u].fail].son[i];
    }
  }
}

代码中 else 部分通过修改字典树的形态，直接把当前点的 fail 的出边情况拉到当前点没有的出边上。
可以手模一下，也可以理解成路径压缩，原本是沿着 fail 跳上去，现在直接把 fail 拉下来了。

怎么进行匹配？

从头遍历文本串的每一位，依次匹配，失配了就跳 fail 。
再偷一下 OI-Wiki 的代码：

int query(const char t[]) {
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u].son[t[i] - 'a'];
    for (int j = u; j && tr[j].cnt != -1; j = tr[j].fail) {
      res += tr[j].cnt, tr[j].cnt = -1;
    }
  }
  return res;
}

能否优化？

可以的，query 时一直跳 fail 太费时间了。
我们可以为找到的节点打上 tag，保留所有的 fail 边，最后做一个内向树拓扑求和即可。
再再再偷一下 OI-Wiki 的代码：

void query(const char t[]) {
  int u = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u].son[t[i] - 'a'];
    tr[u].ans++;
  }
}

void topu() {
  queue<int> q;
  for (int i = 0; i <= tot; i++)
    if (tr[i].du == 0) q.push(i);
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    ans[tr[u].idx] = tr[u].ans;
    int v = tr[u].fail;
    tr[v].ans += tr[u].ans;
    if (!--tr[v].du) q.push(v);
  }
}

把代码拼起来就是【模板】AC自动机

例题

还没做，咕咕咕

病毒

“可以，总司令” 有 60 分。

构造文本串使得所有模式串都未出现在文本串中。

多模式串首先考虑 AC自动机，构建后刻画成功情况：
保证不走到某一模式串末尾的情况下，能走出来一个环即可。
所以标记所有模式串的末尾，然后用 DFS 判环就行。

注意一点：当 fail 的点是某个模式串的末尾时，当前点也一定不行，手模一下即可。

点击查看代码

#include<bits/stdc++.h>
#define N 30010
using namespace std;
struct ACauto{
    struct node{
        int son[2];
        int fail;
        bool c;
        void init(){
            memset(son,0,sizeof(son));
            fail=0;
        }
    }tr[N];
    int tot=0,ans[N],cnt;
    void init(){
        tot=cnt=0;
        tr[0].init();
    }
    void insert(string s){
        int u=0;
        for(char ch:s){
            int &son=tr[u].son[ch-'0'];
            if(!son) son=++tot,tr[son].init();
            u=son;
        }
        tr[u].c=1;
    }
    void build(){
        queue<int> que;
        for(int i=0;i<2;i++){
            if(tr[0].son[i]) que.push(tr[0].son[i]);
        }
        while(!que.empty()){
            int u=que.front();
            que.pop();
            for(int i=0;i<2;i++){
                if(tr[u].son[i]){
                    que.push(tr[u].son[i]);
                    int v=tr[u].fail;
                    tr[tr[u].son[i]].fail=tr[v].son[i];
                    if(tr[tr[v].son[i]].c){
                        tr[tr[u].son[i]].c=1;
                    }
                }else{
                    tr[u].son[i]=tr[tr[u].fail].son[i];
                }
            }
        }
    }
}AC;
int n;
bool vis[N],use[N];
void dfs(int u){
    vis[u]=1;
    for(int i=0;i<2;i++){
        if(vis[AC.tr[u].son[i]]){
            cout << "TAK";
            exit(0);
        }else if(!AC.tr[AC.tr[u].son[i]].c && !use[AC.tr[u].son[i]]){
            use[AC.tr[u].son[i]]=1;
            dfs(AC.tr[u].son[i]);
        }
    }
    vis[u]=0;
}
int main(){
    cin>>n;
    AC.init();
    for(int i=1;i<=n;i++){
        string s;cin>>s;
        AC.insert(s);
    }
    AC.build();
    dfs(0);
    cout << "NIE";
    return 0;
}

阿狸的打字机

暴力很显然，模拟后直接建 AC 自动机，复杂度是高贵的 $O(m|\sum|)$。

然后首先要优化空间，因为每一次都存下来，最后总空间是 $O(n|\sum|)$ 的，也不能接受。
所以我们在 Trie 上额外存一个父亲节点，每次回退时相当于回到父亲的操作，打印时也新开一个标记统计一下末尾节点是第几个出现的字符串。

然后考虑优化时间，容易想到离线按 $y$ 排序，然后把所有相同的 $y$ 一次查完，统一累加。

然后继续想，我们做的是找 $y$ 能经过多少个 $x$，所以直接转化题意成 $x$ 能经过多少个 $y$，题目变成子树求和，dfn序中子树在连续的区间内，所以是区间查询，随便维护一下，可以树状数组或者前缀和。

每次重新 update/重构 一遍的复杂度又劣了，所以我们 DFS 一遍这棵树，每次添加节点后，如果这个节点有 $y$ 的询问，就去 $x$ 上统计子树和，然后回溯的时候把点的贡献删了就行。所以要支持单点修改，选择树状数组。

那么本题就愉快的做完了（难点是将询问转化为子树求和与后续优化）

点击查看代码

#include<bits/stdc++.h>
#define N 100010
using namespace std;
string s;
struct Q{
    int x,y,id,ans;
}q[N];
bool cmp(Q a,Q b){
    return a.y<b.y;
}
int n,a[N],m,ql[N],qr[N];
int dfn[N],dfx,low[N],tot,ans[N];
vector<int> G[N];
struct BIT{
    #define lowbit(i) i&-i
    int t[N];
    void update(int x,int k){
        if(!x) return ;
        for(int i=x;i<=dfx;i+=lowbit(i)){
            t[i]+=k;
        }
    }
    int query(int x){
        int res=0;
        for(int i=x;i;i-=lowbit(i)){
            res+=t[i];
        }
        return res;
    }
}T;
struct node{
    int son[26];
    int vis[26];
    int fail,fa;
    vector<int> id;
}t[N];
void build(){
    queue<int> que;
    for(int i=0;i<26;i++){
        if(t[0].son[i]) que.push(t[0].son[i]);
    }
    while(!que.empty()){
        int u=que.front();que.pop();
        for(int i=0;i<26;i++){
            if(t[u].son[i]){
                t[t[u].son[i]].fail=t[t[u].fail].son[i];
                que.push(t[u].son[i]);
            }else{
                t[u].son[i]=t[t[u].fail].son[i];
            }
        }
    }
}
void dfs(int u){
    dfn[u]=++dfx;
    for(int v:G[u]){
        dfs(v);
    }
    low[u]=dfx;
}
void dfs2(int u){
    T.update(dfn[u],1);
    if(t[u].id.size()){
        for(int j=0;j<(int)t[u].id.size();j++)
            for(int i=ql[t[u].id[j]];i<=qr[t[u].id[j]];i++){
                q[i].ans=T.query(low[a[q[i].x]])-T.query(dfn[a[q[i].x]]-1);
            }
    }
    for(int i=0;i<26;i++){
        if(t[u].vis[i]){
            dfs2(t[u].vis[i]);
        }
    }
    T.update(dfn[u],-1);
}
int main(){
    cin>>s;
    int u=0;
    for(char ch:s){
        if(ch<='z' && ch>='a'){
            int &son=t[u].son[ch-'a'];
            if(!son) son=++tot,t[tot].fa=u;
            u=son;
        }
        if(ch=='B') u=t[u].fa;
        if(ch=='P') {a[++n]=u;t[u].id.push_back(n);}
    }
    for(int i=0;i<=tot;i++){
        for(int j=0;j<26;j++){
            t[i].vis[j]=t[i].son[j];
        }
    }
    build();
    for(int i=1;i<=tot;i++){
        G[t[i].fail].push_back(i);
    }
    dfs(0);
    cin>>m;
    for(int i=1;i<=m;i++){
        cin>>q[i].x>>q[i].y;
        q[i].id=i;
    }
    sort(q+1,q+1+m,cmp);
    int pos=1;
    for(int i=1;i<=m;i=pos){
        ql[q[i].y]=i;
        while(q[i].y==q[pos].y) pos++;
        qr[q[i].y]=pos-1;
    }
    dfs2(0);
    for(int i=1;i<=m;i++) ans[q[i].id]=q[i].ans;
    for(int i=1;i<=m;i++) cout << ans[i] << '\n';
    return 0;
}

Divljak

如果没有修改，就是板子题，fail 树上统计子树和就行，所以考虑修改。

肯定不能插入就重新 buildfail，时空双爆炸。

再读题发现询问的集合只有最开始给出的 $n$ 个字符串，所以对 S 做 AC自动机。
当我们拿字符串 P 在 AC自动机上走的时候，相当于枚举 P 的前缀，对应的节点 u 则是 P 的前缀匹配的最长后缀，然后跳 fail 过程经过的节点，都是 P 的子串。
所以 P 的贡献其实是 P 能到达的点集 $V={v_1,v_2…v_p}$ 到根节点的所有链的并集。
根据之前的一道题（寻宝游戏）可知，树上若干点组成的路径，是这几个点按 dfn 排序后，相邻两点的路径长度。
运用这个技巧，排序后就变成 链加 和 单点查 了。这个时候就可以大力树剖+线段树。
当然可以偷懒用树上差分转为 单点修 和 子树和 用树状数组维护一下。

点击查看代码

#include<bits/stdc++.h>

using namespace std;
const int N=1e5+10;
const int M=2e6+10;
vector<int> G[M];
struct acauto{
    struct node{
        int son[26];
        int fail,cnt;
    }tr[M];
    int tot=1,en[N];
    void insert(const string &s,int idx){
        int u=1;
        for(char ch:s){
            int &son=tr[u].son[ch-'a'];
            if(!son) son=++tot;
            u=son;
        }
        tr[u].cnt++;
        en[idx]=u;
    }
    void build_fail(){
        for(int i=0;i<26;i++){
            tr[0].son[i]=1;
        }
        queue<int> que;
        que.push(1);tr[1].fail=0;
        while(!que.empty()){
            int u=que.front();que.pop();
            for(int i=0;i<26;i++){
                if(tr[u].son[i]){
                    tr[tr[u].son[i]].fail=tr[tr[u].fail].son[i];
                    que.push(tr[u].son[i]);
                }else{
                    tr[u].son[i]=tr[tr[u].fail].son[i];
                }
            }
        }
    }
}AC;
struct BIT{
#define lowbit(i) i&-i
    int tr[M];
    void update(int x,int k){
        if(!x) return ;
        for(int i=x;i<=AC.tot;i+=lowbit(i)){
            tr[i]+=k;
        }
    }
    int query(int x){
        int res=0;
        for(int i=x;i;i-=lowbit(i)){
            res+=tr[i];
        }
        return res;
    }
}T;
int dep[M],siz[M],hson[M],top[M],fa[M],dfn[M],dfx;
void dfs1(int u,int pa){
    dep[u]=dep[pa]+1;fa[u]=pa;
    siz[u]=1;
    for(int v:G[u]){
        if(v==pa) continue;
        dfs1(v,u);
        siz[u]+=siz[v];
        if(siz[v]>siz[hson[u]]) hson[u]=v;
    }
}
void dfs2(int u,int tp){
    top[u]=tp;
    dfn[u]=++dfx;
    if(!hson[u]) return;
    dfs2(hson[u],tp);
    for(int v:G[u]){
        if(v==fa[u] || v==hson[u]) continue;
        dfs2(v,v);
    }
}
int LCA(int x,int y){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        x=fa[top[x]];
    }
    return dep[x]>dep[y] ? y : x;
}
bool cmp(int a,int b){
    return dfn[a]<dfn[b];
}
int n,q,tmp[M],cnt;
string s;
int main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>s;
        AC.insert(s,i);
    }
    AC.build_fail();
    for(int i=2;i<=AC.tot;i++){
        G[AC.tr[i].fail].push_back(i);
    }
    dfs1(1,0);dfs2(1,1);
    cin>>q;
    for(int i=1,op;i<=q;i++){
        cin>>op;
        if(op==1){
            cin>>s;
            int u=1,cnt=0;
            for(char ch:s){
                u=AC.tr[u].son[ch-'a'];
                tmp[++cnt]=u;
            }
            for(int i=1;i<=cnt;i++){
                int a=tmp[i];
                T.update(dfn[a],1);
            }
            for(int i=1;i<cnt;i++){
                int a=tmp[i],b=tmp[i+1];
                T.update(dfn[LCA(a,b)],-1);
            }
        }else{
            int x;
            cin>>x;
            int idx=AC.en[x];
            cout << T.query(dfn[idx]+siz[idx]-1)-T.query(dfn[idx]-1) << '\n';
        }
    }
    return 0;
}